CSE 232 - Databases Systems
- Lecture 1
- Lecture 2 - Database Storage and Hardware Design
- Lecture 3 - Indexing
- Lecture 4 - Indexing Pt. 2
- Lecture 5 - Indexing Pt. 3 - Hashing
- Lecture 6 - Query Processing
- Lecture 6 - Relational Algebra Optimization
- Commutativity and Associativity
- Rewriting of algebraic expressions for logical connectives
- Pushing Selection Through Binary Operators: Union and Difference
- Pushing Selection Through Cartesian Product and Join
- Pushing Projections Through Binary Operators
- Pushing Projections Through Join and Cartesian Product
- Deriving some rules
- What are always “good” transformations?
- Examples
- The Bottom Line
- Algorithms for Relation Operators
- Pipelining can greatly reduce cost.
- Iteration Join
- Lecture 7 - Joins with Indexes
- Lecture 8 - Estimating the Cost of a Query Plan
- Lecture 9 - Plan Enumeration
- Lecture 10 - Failure Recovery
- Lecture 11 - Transactions Cont’d
- Lecture 12 - Transaction Concurrency Control Cont’d
- Lecture 13 - Concurrency Control Cont’d
- Lecture 14 - More Concurrency Control and Transactions
- Lecture 15 - Query Processing …Again
Lecture 1
Lecture 2 - Database Storage and Hardware Design
- Different storage types used by databases
- Typically cost is higher and amount of storage is lower the faster it is
- CPU-level cache typically isn’t controlled by the software, so the DB can’t do much optimization around it
- RAM is utilized by DB, but can’t guarantee transactions due to volatility
- SSD, HDD, Tape, etc are non-volatile and can guarantee transactions
Peculiarities of storage and algorithms
- most storage is accessible via block-based access (via kernel, i.e. block device)
- not just pulling the bytes we need - taking big chunks.
- clustering (for hard disks):
- cost is lower for consecutive blocks.
- sequential read times have increased immensely
- minimum access time to first byte has not decreased propotionally
Ex: 2-phase merge sort
- Pass 1: Read section by section into buffer, sort all data, write sorted section to file
- 2nd pass: file pointers to all previously written files, read block from each file write in sorted order out to new file.
- Assume RAM buffer of size \(M\)
- Block size of $$B$
- Number of block reads = \(M/B\)
- File sections: \(N / M / B\)
With ram buffer of size \(M\) can sort up to \(M^2 / B\) records (at least one block from each ram buffer)
Horizontal Placement of SQL data in blocks
- row oriented - tuples packed together in blocks
- improve total table scan time
- for deletions, clear the block, add a “mark” (bit?) for deletion
- for additions to a sorted table by a key, leave a pointer on the block where it should exist to the new record (only applies on sorted files)
Lecture 3 - Indexing
Given condition on attribute, find the qualified records
- Indexing is a trick to speed up the search for attributes with a particular
value
- Conditions may include operations like
>,<,>=,<=, etc
- Conditions may include operations like
- Different types of indexes, each need evaluation
- time for access, insert, delete, or disk space
Topics
- Conventional (Traditional) Indexes
- B-Trees
- Hashing Schemes
Terms and Distinctions
- Primary Index - index on the attributes which determines sequencing of the
table.
- can tell if value exists without accessing a file
- easier access to overflow records (refer to previous lecture)
- required for secondary index
- Secondary Index - indexes on any other attribute
- sparse index takes lest space.
- better insertions
- Dense Index - every value of the indexed attribute appears in the index
- Sparse Index - many values do not appear
Can have multi-level indexes
- index the index!
- generally, two-level index is sufficient, more is rare
Pointers - a block pointer, value of record attribute, then a value representing the block and/or record location.
- Block pointers cannot be record identifiers
What if a key isn’t unique?
- Deletion from a dense primary index with no duplicate is the same way as a sequential file - leave blank space
- Deletion from a sparse index, similar approach, but might not have to delete
anything.
- or, simply leave it, just change the pointer without changing any blocks
- must assume the algorithm doesn’t assume a value exists just because it exists in the index.
- or, simply leave it, just change the pointer without changing any blocks
Insertion in sparse index: if no new blocked is created for the key, do nothing
- otherwise, create an overflow record
- reorganize periodically
Duplicate values and secondary indexes
- option 1: index entry to each tuple. not very efficient
- option 2: index on unique values, then have blocks of “buckets” containing sequential pointers to duplicate values
Why bucket+record pointers is useful
- enabled processing of queries working with pointers only
- common technique in information retrieval
- with buckets and record pointers, can simply do set intersection of record
pointers in order to answer query
- read less data blocks
B+Trees
- Give up on sequential records, try to achieve balance instead
- “node” and “block” are equivalent in lecture
- node with three values \(j, k, l\), 4 pointers (\(n+1\))
- \[p1 < j\]
- \[j >= p2 > k\]
- \[k >= p3 > l\]
- \[l >= p4\]
- non-root nodes must be at least half-full
- non-leaf node \(\lceil \frac{n+1}{2} \rceil\) pointers
- leaf node: \(\lfloor \frac{n+1}{2} \rfloor\).
- bounded number of block access in the index based on the depth of the tree
Lecture 4 - Indexing Pt. 2
- Coalescing and deletes in B+Trees are not always implemented.
- Play with https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html for visualizations.
- Important to note again why B+ trees are important: guaranteed bound on block accesses to get to leaf node
Hashing Schemes
- hashing returns the address of bucket
- In the case of key collisions, the bucket is a linked list
- compute the table location as \(hash(key) % buckets\)
- sorting in buckets only if cpu time for lookup is critical and inserts+deletes are not frequent
- in DBs, hashing limited by data blocks to limit lookup accesses (different
from array-based hash map in languages like Java)
- entries in the buckets (blocks) have the key and a pointer to the corresponding data location.
- if a bucket overflows too much, there is a pointer to an overflow block.
- Rule of thumb: keep space utilization between 50% and 80% to limit overflow
creations.
- \(< 50%\) wasting space
- \(> 80%\) slow down lookups due to overflow buckets
- How to cope with growth?
- Overflow blocks make it slow to lookup
- re-hashing wastes lots of time
Extensible Hashing
- Extensible Hashing: 2 ideas
- use \(i\) of \(b\) bits which are output by the hash function.
- use a directory to point to buckets
- directory fits in main memory
- points to buckets which contains full keys+pointer
- When you overflow a bucket, increase the number of bits, \(i\) that the hashed values agree on, then create a new directory table without modifying the original blocks, and placing the new block from the block where records overflowed with the transferred records.
- Strengths
- Can handle growing files
- less wasted space
- no full reorganization
- Can handle growing files
- Weaknesses
- Reorganizing table can be expensive
- Indirection, not bad if everything in main memory
- directories double in size
Linear Hashing
- keep same idea of using low order bits from hash value
- file grows in linear fashion
- Variables
- keys of \(b\) bits
- hash bits of \(i\)
- n keys in data blocks (again)
- \(m\) to track maximum used block.
- Rule
\(h(k)[i] \leq m \text{ bucket } h(k)[i]\)
-
else \(h(k)[i] - 2^{i-1}\)
- When to expand the file?
- keep track of \(\frac{\text{# used slots (incl. overflow)}}{\text{# total slots in primary buckets}}\)
- when above a threshold, increase \(m\), as well as \(i\) when \(m = 2^i\)
- Strengths
- can handle growing files
- less wasted space
- no full reogranization
Lecture 5 - Indexing Pt. 3 - Hashing
- Indexing vs hashing
- Hashing is a good to probe for a specific key
- Indexing (b+tree) is good for range searches
- DBs tend to have tree-based indices because it makes it easy to implement predicates with greater, less, leq (less than eq.), geq
- Traditional DBs don’t really let you define the types of indexes (b-tree/hash)
in SQL
- Some systems allow configuration parameters to change implementation
- Multi-key indices to speed up queries with conditions on multiple attributes
- Strategy for multi-condition queries with single index on each attribute
- use one index and get tuples to satisfy cond1
- iterate over list from above result to return correct set
- another strategy
- multi-index, find set of results satisfying both, then perform set intersection logic to get result (AND) condition.
- use one index and get tuples to satisfy cond1
- Instead, structure keys as trees.
- At the top level, sort by first key
- all tuples underneath top-level attribute in a group, have same attribute value for top-level key.
- At the top level, sort by first key
- Strategy for multi-condition queries with single index on each attribute
Bitmap Indices
- Heavily used in OLAP (online analytics)
- Assume that tuples are in some order that each index sees globally
- e.g. each index attribute value has a bitmap (string of 1’s and 0’s) e.g. given a table
| name | dep | year |
| aaron | suits | 4 |
| helen | pens | 3 |
| jack | PCs | 4 |
| yannis | pens | 1 |
then our bitmaps indices would be
| dept | bitmap |
| PCs | 0010 |
| pens | 0101 |
| suits | 1000 |
| year | bitmap |
| 1 | 0001 |
| 2 | 0000 |
| 3 | 0100 |
| 4 | 1010 |
- unfortunate, bitmaps require a lot of space
- increase in size w/ number of tuples
- for 1B tuples, 1B / 8 bytes of space * number of values for the index
- can try to compress bitmaps! (mostly 0’s)
- Compression
- naive solution for bitmap requires \(n*m\) bits
- in reality, across the whole map there is only \(n\) 1’s
- compress bitmap to \(2nlog(m)\)
- \(n\) is the number of tuples
- \(m\) is the number of distinct values.
- e.g. 00011010 compresses to 301
- 3 0’s until first 1
- 0 0’s until 2nd 1
- 1 0 until 3rd 1
- further compress the encoding of the bitmap
- 301 binary representation (digit-wise)
- 11 (2 bits, 10 in binary)
- 0 (1 bits)
- 1 (1 bits)
- end length scheme with 0, fill # of bits before - 1 with 1’s
- eg. encode
10010-> 1111010010
- eg. encode
- 0’s act as delimiters
- Represent this as
- 10110001
- 301 binary representation (digit-wise)
Bitmap example 2:
Pens bitmap: 01000001
Sequence: [1, 5]
Encoding: 01110101
- Handling Insertions and Deletions
- Assertions, assume happens in order (nothing to do)
- Deletions: do nothing, leave record and 0-out bitmap
- Insertions: if tuple t with value v is inserted, add one more run in v’s sequence.
Proving 2*nlog(m)
- n * m bits
- will find exactly \(n\) runs. (Across all bitmaps)
- why is the average run length \(2*log(m)\)?
- \(n\) bits per bitmap - expect average \(\frac{n}{m}\)
- n / (n / m) -> size of conceptual bitmap divided by the average run size -> \(m\)
Lecture 6 - Query Processing
- A query processor turns user queries and data modification commands into a
query plan
- query plan is a sequence of operations on the database
- Decisions taken by a query processor
- which of the algebraically equivalent forms of a query will lead to the most efficient algorithm?
- for each algebraic operator, what algorithm should we use to run the operator
- how should the operators pass data from one to the other?
Example
SELECT B, D
FROM R,S
WHERE R.A = "c" and S.E = 2 AND R.C = S.C
How to execute this query?
- idea 1:
- scan relations
- do a cartesian product
- select tuples
- do projection
Use relational algebra to describe the plan: e.g.
- \[\Pi^{FLY}_{B,D}[\sigma^{FLY}_{R.A="c" \land S.E=2 \land R.C=S.C}(R^{SCAN} \times S^{SCAN})]\]
Above is very inefficient…
- Plan 2: Instead of a full scan with a cartesian product, we can do something
different:
- scan each table and only include rows matching the predicates in the result
- perform natural hash join on reduced tables
- Plan 3: use indexes of each table
- use R.A index to select tuples of
R.A = "c" - for each
R.Cvalue found, useS.Cindex to find matching joins - eliminate join tuples where
S.E != 2 - projection
- use R.A index to select tuples of
- From query to optimal query plan
- complex
- algebra based logical and physical plans
- transformations
- may need to evaluate alternatives
- Issues in query planning:
- generating plans
- employ efficient primitives to compute these operations
- estimate cost of plans
- “smart” search of possible plans
- generating plans
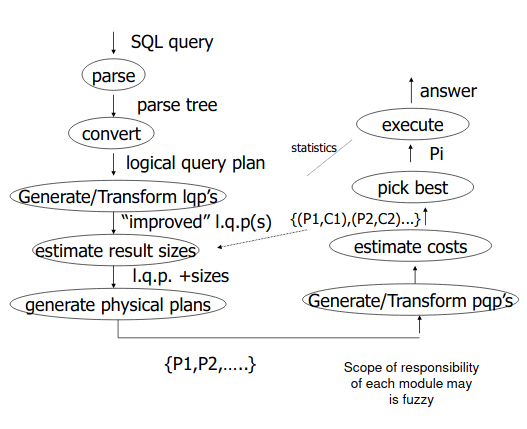
Algebraic Operators
Predicates (\(\sigma\))
- Select tuples of \(R\) that satisfy condition \(C\): \(\sigma^R_C\)
- may contain multiple condition with AND/OR
- may be of the for
attr1 = valueorattr1 = attr2 - other operators like \(<,>,\neq,\text{LIKE}\)
Projections (SET vs BAG): \(\Pi\)
- \(\Pi_{a_1...a_n}^{R}\):
- returns a table that has only attributes \(a_1\),…,\(a_n\) of \(R\)
- Set version: no duplicate tuples in the result
- Bag version: allows duplicates
Cartesian Product: \(\times\)
- \(\times\):
- the schema is the combination of all attributes of \(R\) and \(S\)
- for every tuple in \(R\) is matched to all tuples of \(S\)
- if there are any attribute name collisions, prefix with the
<Table_Name>.
Algebraic Operators: A Bag Version
- Union of R and S: a tuple t is in the result as many times as the sum of the number of it is in R, plus the times it is in S.
- Intersection of R and S: A tuple t is in the result the minimum number of time it is in R and S.
- Difference of R and S A tuple t is in the result the number of times it is in R minus the number if times it is in S.
- \(\delta(R)\) converts the bag \(R\) into a set.
The Extended Projection
- Extend the relation projection \(\pi_A\):
- the attribute list may include \(x\rightarrow y\) in the list to indicate the attribute x is renamed to y
- Arithmetic, string operators, and scalar function on attributes are allowed
- e.g. \(a+b\rightarrow x\) means teh sum of a and b is renamed to x.
- e.g. \(c||d\rightarrow y\) concatenates teh result of c and d into a new attribute named y.
- Note these are available only for scalar functions - not aggregations (like AVERAGE, COUNT).
- results are generated by computing a new tuple with any renamed attributes and functions applied.
Example
SELECT 2*A, as D, B, C as CPRIME
FROM T
would be converted into
\[\pi_{2A\rightarrow D,B,C\rightarrow CPRIME} T\]Cartesian Products -> Joins
- Product of R and S (\(R\times S\))
- if an attribute named a is found in both schemas, the rename by prefix
- if a tuple r is found n times in R and a tuple s is found m times in S then the product contains nm instances of tuples rs.
- Joins
- Natural Joins: \(R \bowtie S\rightarrow \pi_{A}\sigma_{C}(R\times S)\)
- C is a condition that equates common attributes
- A is the concatenated list of attributes of R and S with no duplicates
- Theta Join
- arbitrary condition that involves multiple attributes
- Natural Joins: \(R \bowtie S\rightarrow \pi_{A}\sigma_{C}(R\times S)\)
Example of a theta join
SELECT T.A
FROM T,S
WHERE T.A=S.B
equates to
\[\pi_{T.A} (T \theta_{T.A=S.B} S)\]Grouping and Aggregation: \(\gamma\)
- \[\gamma_{\text{groupByList};\text{aggrFn1}\rightarrow \text{attr1}}\]
- Conceptually, grouping leads to nested tables and is immediately followed by functions that aggregate the nested table.
- example: \(\gamma_{\text{dept.;AVG(Salary)}\rightarrow\text{AvgSal},\text{SUM(Salary)}\rightarrow\text{SalaryExp}}\)
Example 2:
SELECT Dept, AVG(Salary) AS AvgSal
FROM Employee
GROUP BY Dept
HAVING SUM(Salary) > 100
Sorting and Lists
- SQL and algebra results are ordered
- Could be non-deterministic or dictated by SQL’s
ORDER BY(\(\tau\)) - A result of algebraic expression o(exp) is ordered if
- o is \(\tau\)
- if o retains ordering of exp and exp is ordered
- depends on implementation !
- if o creates ordering
- consider leaf of tree may be scan (R)
Lecture 6 - Relational Algebra Optimization
- Work with algebras - transform one expression to another equivalent
- simple example \(x(y + z) = xy + xz\)
- Need to determine which are “good” transformations
Commutativity and Associativity
- Commutative: \(R \times S = S \times R\)
- Associative: \(R \times (S \times T) = (R \times S) \times T\)
-
Natural join (\(\bowtie\)) is also commutative and associative
- Commutative
- cartesian product: \(\times\)
- natural join/theta join: \(\bowtie\)
- union: \(\cup\)
- intersection: \(\cap\)
- Associative
- cartesian product: \(\times\)
- natural join/theta join: \(\bowtie\)
- union: \(\cup\)
- intersection: \(\cap\)
Rewriting of algebraic expressions for logical connectives
instructor not clear on this section. refer to slides
Pushing Selection Through Binary Operators: Union and Difference
- \[(R \cup S) \sigma_\text{cond} = \sigma_\text{cond} R \cup \sigma_\text{cond} S\]
- \[(R - S) \sigma_\text{cond} = (\sigma_\text{cond} R) - (\sigma_\text{cond} S)\]
Pushing Selection Through Cartesian Product and Join
- \[(R \times S) \sigma_\text{cond} = R \times (\sigma_\text{cond} S)\]
- \[(R \bowtie S) \sigma_\text{cond} = R \bowtie (\sigma_\text{cond} S)\]
Pushing Projections Through Binary Operators
- \[(R \cup S) \pi_A = (\pi_A R)\cup(\pi_A S)\]
Pushing Projections Through Join and Cartesian Product
-
\[(R\times S)\pi_A = ((R\pi_B) \times (S\pi_B))\pi_A\]
- same for natural join
Deriving some rules
- \[\sigma_{p\land q} (R \bowtie S) = \sigma_p R \bowtie \sigma_q S\]
- see more examples in slides
What are always “good” transformations?
- Some transformations are always good
- others we do because it creates alternative (new) transformations which can also be efficient.
Examples
-
\[\sigma_{p1\wedge p2}(R) \rightarrow \sigma_{p1} (\sigma_{p2}(R))\]
- not always good because conditions depend on index
-
\[\sigma_p(R\bowtie S) \rightarrow (\sigma_p (R)) \bowtie S\]
- Usually good because joins are expensive, good to eliminate first.
The Bottom Line
- No transformation is always good
- Usualy good:
- early selections
- elimination of cartesian products
- elimination of redundant subexpressions
- many transformations can lead to “promising” plans
- communicating/rearranging joins
- in practive, too combinatorially explosive to handle a re-writing
Algorithms for Relation Operators
- 3 Primary techniques
- sorting
- hashing
- indexing
- 3 degrees of difficulty
- data small enough to fit in memory
- too large to fit in main memory, but small enough to be handled by a two-pass algorithm
- so large that two-pass methods have to be generalized to multi-pass
- Dominant cost of operators running on disk
- no. of disk block that must be read/written to execute query plan
Pipelining can greatly reduce cost.
- each operator can scan through file with tuples
- check condition (select) with sigma
- project with pi
- intermediate files between steps
- open/close between each
- (this is very very slow)
- Instead, pipeline operators while opening data files
- pass output from one operator into the next operator
- no intermediate files
Iteration Join
- \(R1 \bowtie R2\) on a common attribute C
- Least efficient iteration join
for r in R1:
for s in R2:
if r.C = s.C, output (r, s)
- merge join (conceptual)
- if R1 and R2 not sorted by C, sort them
- dual pointer algorithm
- move smaller value pointer to next tuple
- emitting pairs until hitting the end of the smaller table
- however, slightly more complex, as you need to keep track of
sets of equivalent values
- need to output all combinations of tuples
- dual pointer algorithm
- O(n+m)
- if R1 and R2 not sorted by C, sort them
Lecture 7 - Joins with Indexes
- Join with index (conceptual)
- Hash join
- hash function range \(0\rightarrow k\)
- buckets for R1 into G buckets
- buckets for R2 into H buckets
- Algorithm
- hash all R1 tuples into G buckets
- hash all R2 tuples into H buckets
- for i = 0 to k
- match tuples in \(G_i = H_i\)
- small joins on buckets
- in postgres, “hash join” oriented is actually kind of like an index join with an ephemeral hash index
Disk Oriented Computation Model
- \(M\) main memory buffers
- each buffer is the size of a disk block
- assume input of relation is read one block at a time
- assume dominant factor is IO, and the number of blocks read directly
correlates to time
- assumption is fine for SSD
- For HDD consecutive is very different from random
- assume output buffers are not part of M buffers mentioned above
- Pipelining allows the output buffers of an operator to be the input to the next operation
- do not count the cost of writing output
- Future cost notation
- \(B(R) =\) number of blocks on disk that R occupies
- \(T(R) =\) number of tuples in R
- \(V(R,[a_1, a_2,\dots,a_n]) =\) number of distinct tuples in the projection of R on \(a_1, a_2,\dots,a_n\)
- One-pass main memory algorithms for unary operators
- Assumption: enough memory to keep entire relation in memory
- Projection
- scan R, apply operator to one tuple at a time
- incremental cost of “on the fly” operators - 0 (no additional disk operators, aside from needing to read data at least once to produce the result)
- Duplicate Elimination and Aggregation
- Create one entry for each group, compute aggregated group value
- hard to assume CPU cost is negligible here
- require “complex” data structures
- Create one entry for each group, compute aggregated group value
- One pass nested loop join
- cost is simply \(B(R) + B(S)\) because you simply loop over all tuples of each table once to join (since everything fits in memory)
- Simple Sort-Mege Join
- Assume R natural join on S on attribute C
- Algorithm
- Read and sort R on C
- Read and sort S on C
- Merge using two pointer algorithm
- Cost assuming both tables not previous sorted and a 2-pass multiway merge
sort is used
- sort cost is \(4B(T)\rightarrow 4B(R) + 4B(S)\) (sort is 2x read, 2x write)
- join cost is B(R) + B(S)
- total cost is \(5B(R) + 5B(S)\)
- Can we do better though?
- Save two disk IOs per block by combining second pass sorting with merge
- create sorted sublists of size M for R and S
- bring first block of each sublist into a buffer
- repeatedly find the leaste C value among the first tuples of each
sublists. Identify all tuples with a join value c, and join them
- when a buffer has no more tuples that has not already been considered, load another block into this buffer.
- by joining on the final phase of merge sort, the cost is reduced \(3B(R)+3B(S)\)
- Hash Join Algorithms
- Assuming a natural join, use a hash function that is the same for both input arguments, and only uses join attributes
- Algorithm:
- Phase 1: Hash each tuple of R into one of the \(M-1\) buckets \(R_i\) and similarly for S
- Phase 2: For i=1..M-1
- load \(R_i\) and \(S_i\) in memory
- join and save result to disk.
- Cost: \((2B(R) + 2B(S)) + (B(R) + B(S))\)
- Index-Based Join: Simple Version
- Assume natural join of R and S where the index is on S
- Algorithm:
- read a block of R
- for each tuple in the block use the index of S to find the tuples of S with value b
- read a block of R
- Assuming R is not sorted and S is indexed and clustered on B
- Cost of \(B(R) + T(R)B(S)/V(S,B)\)
- If R is sorted, find all tuples of R with a given b value, then issue index access
Lecture 8 - Estimating the Cost of a Query Plan
Requires
- Esimating the size of results
- Estimating the number of IOs
Estimating result size: need the following statistics
- T(R): the number of tuples in R
- S(R): number of bytes in each tuple of R
- B(R): number of blocks to hold all R tuples
- V(R, A): number of distinct values for attribute A in R
Ex:
Given \(W = R1\times R2\)
- \[T(W) = T(R1) \times T(R2)\]
- \[S(W) = S(R1) + S(R2)\]
Size estimate for $$W = \sigma_{Z=val}(R)
- S(W) = S(R)
- T(W) = T(R) / V(R, Z)
Calculating Results with Inequalities
What about a query \(W = \sigma_{z \geq 15}R\)?
- Keep statistics on the table, a histogram of frequencies over a number of buckets
Size estimate of a join…
- query: \(W = R1\bowtie R2\)
- Let X = attributes of R1
-
ket Y = attributes of R2
- Join can have \([0, T(R1)T(R2)]\) tuples.
- If we have some more information it can be helpful
- Assume every value of A in R1 is in R2 (typically A is a foreign key of R1, R2.A is a primary key)
Computing T(W) when A of R1 is a foreign key of R2
-
If R2.A is a primary key, it occurs only once, so then the T(W) = T(R1)
-
Ok, but what happens when A is not a primary key (unique), then we need to multiple T(R1) by the average number of matches in R2. Thus
- in the case of \(V(R1, A) \leq V(R2, A) \rightarrow T(W) = \frac{T(R2)T(R1)}{V(R2, A)}\)
-
in the case of \(V(R2, A) \leq V(R1, A) \rightarrow T(W) = \frac{T(R2)T(R1)}{V(R1, A)}\)
- In general \(T(W) = \frac{T(R2)T(R1)}{max(V(R1, A), V(R2, A))}\)
Case: A 3-way join for 3 tables which share the same attribute?
Example:
R1, R2, R3
- T(R1) = 10000
- T(R2) = 20000
- T(R3) = 5000
- V(R1, A) = 1000
- V(R2, A) = 20000
- V(R3, A) = 500
Join: \(R1\bowtie R2\bowtie R3 \rightarrow (R1\bowtie R2) \bowtie R3\)
- The intermediate result of \(R1\bowtie R2\) has \(T(R1\bowtie R2) = 10000\)
- The intermediate of \(V(R1\bowtie R2, A) =\)1000, or 20,000?
- Preserve probability of the larger table?
- The intermediate of \(V(R1\bowtie R2, A) =\)1000, or 20,000?
Lecture 9 - Plan Enumeration
- Smart exhaustive algorithm for generating query plans
- Textbook Section 16.6
- INGRES Heuristic for enumeration
Practice problems
Given the relations R(A, B, C) and S(C, D, E) give 6 valid logical query plans
SELECT B, C, D
FROM R, A
where R.C=S.C AND R.A=5;
Given the relations R, S, and T, Give an algebraic expression that only contains the join operator
SELECT *
FROM R, S, T
where R.A=S.A AND S.B=T.B;
Given the plans from the above problem, give plans for executing the query.
- To generate a query plan, pick one of the types of algorithms for join operators
- e.g.
- Hash Join (HJ)
- Sort Sort Merge (SSM)
- **M (merge only if sorted)
- *SM (sort only one)
- S*M (sort only one)
- e.g.
Arranging the Join Order: Wong-Yussefi Algorithm
- Challenges with large natural join expressions
- for simplicity, assume that in the query
- all joins natural (equality conditions)
- whenever two tables of the FROM clause have common attributes, we oin them
- consider right-index only
- assume that on join operator, the right-hand argument has an index key that maps directly to the index of the left-hand operand.
- for simplicity, assume that in the query
- Wong-Yussefi assumptions and objectives
- assumption 1 (weak): indexes on all join attributes (keys+foreign keys)
- assumption 2 (strong): at least one selection creates a small relation
- joins on small relations results in a small relation
- objective: create a sequence of index-based joins such that all intermediate results are small.
- Calculates cost via “hypergraph” data structure
- nodes are attributes
- relations are hyperedges
- pick small relation (and conditions) to start the plan.
- Remove the small relation (hypergraph reduction) and color as many small relations that join with the removed “small” relation
- What happens if there are multiple foreign keys? multiple selections?
- multiple options to follow in the hypergraph.
- generally, pick smallest items before joining on larger tables.
- multiple options to follow in the hypergraph.
- Algorithm has generally good ideas, but does not really survive because it
makes too many assumptions
- new approach, use dynamic programming to enumerate plans.
Lecture 10 - Failure Recovery
- Integrity and correctness of data is of utmost importance
- Integrity+consistency constraints
- some predicates DB must satisfy:
- x is key of R
- x –> Y holds in R
- domain(x) = {R, G, B}
- no employee should make more than twice the average salary
- these types of consistency are based on business logic constraints.
- DB builders are concerned with the view of data pre and post transaction are consistent.
- some predicates DB must satisfy:
- Transaction: a collection of actions that preserve DB consistency
- Working assumption for transactions:
- if T starts with a consistent state, and T executes until completion and isolation, then T leaves a consistent state.
- How to prevent and fix violations?
- failure recovery: fixing violations due to failures
- concurrency control: fixing violations due to concurrency and data sharing
- a mix: fixing violations that stem from interaction of failures with sharing
- What is not considered in this class
- how to write correct transactions (buggy transactions can violate constraints)
- how to write a correct dbms
Failure Model
- Events
- desired
- undesired
- expected
- memory loss
- cpu halt, crash, reset
- unexpected (db crash)
- disk data lost, memory lost without CPU halt, skynet CPU decides to wipe out programmers….
- expected
Storage Hierarchy
- memory <–> disk
- operations:
- input(x) block with X –> memory
- output(x) block with X –> disk
- read(x, t): input (x) if necessary, t <– value of X in block
- write(x, t): input(x) if necessary, value of X <– t
- key problem: unfinished transactions
- constraint: A=B
- \[T_1 \leftarrow A\times 2 \rightarrow B\leftarrow B\times 2\]
- if db crashes before all updates a written, on recovery we could have onconsistent state of disk.
- need ability to execute “all or none” semantics
- undo logs of unfinished transactions
- use a commit log to log all changes to DB
- complications
- log first written to mem, not written to disk on every action (too expensive)
- complications
- undo logging rules
- for every action, generate an undo log record (containing old value)
- before x is modified on disk, log records pertaining to x must be on disk (Write-ahead-log, WAL)
- before commit is flushed to log, all writes of transaction must be reflected on disk.
- recovery rules: undo logging:
- let S = set of transactions that have a start log but no commit (or maybe an abort log)
- for each transaction statement, in reverse order (latest to earliest)
- if \(T_i\) in the set of transactions then (write(X, v), output(X))
- for each transaction, write a transaction abort to log.
- What about failure during recovery?
- undo is idempotent, can replay again.
- Redo logging
- do transactions, but don’t output results until the transaction is committed in the log.
- rules
- for every action, generate a redo log record
- before X is modified on disk, all log records for transaction that modified X (including final commit) must be on disk
- flush log at commit.
- recovery rules
- Let S be a set of transactions with a commit entry in the log
- for each transaction statement in forward order (earliest to latest) do
- write(X, v)
- Output(X)
- recovery is slow
- checkpoint to speed up
- periodically:
- do not accept new txns
- wait until all txns finish
- flush all log records
- flush all buffers
- write checkpoint record
- resume txns
- periodically:
- key drawbacks
- undo logging:
- cannot bring backup DB copies up to date, real writes at end of txn needed
- redo logging:
- need to keep all modified block in memory until commit.
- undo logging:
Lecture 11 - Transactions Cont’d
- how to address issues from last lecture?
- undo/redo logging! (use both)
- rules
- page X can be flushed before or after commit \(T_i\)
- log record can be flushed before corresponding updated page
- flush at commit (log only)
- problem: at boot up, need to replay committed transactions
- can checkpoint so that the log doesn’t grow too large
- problem with naive checkpoint is that working to establish a checkpoint needs database downtime.
- solve problem with non-quiescent checkpoint
- non-quiescent checkpoint
- start checkpoint, but take note of active transactions.
- on DB recovery, undo transaction statements that began before or after checkpoint, and didn’t complete
- redo transaction blocks that were written after checkpoint start but where transaction already began
- recovery process summary
- backwards pass (end of log to latest checkpoint start)
- construct set of S committed transactions
- undo actions of transactions not in S
- undo pending transactions
- follow undo chains for transactions in (active checkpoint list) - S
- forward pass (latest checkpoint start to end of log)
- redo actions of S transactions.
- real-world actions
- execute real-world actions (e.g. subtracting from bank account balance)
after commit
- want actions to be idempotent
- execute real-world actions (e.g. subtracting from bank account balance)
after commit
- summary
- transaction processing for keeping DB consistent
- source of problem: DB/hardware failures
- use logging + redundancy
- next source of problems: concurrency and data sharing
- source of problem: DB/hardware failures
- transaction processing for keeping DB consistent
Intro to Concurrency Control
- DBs usually have many processes communicating with the DB with multiple Txns in parallel.
- concurrency control: how to best interleave reads and writes to maintain consistency
- want transaction schedules that are “good”
- equivalent to serial execution regardless of
- initial state
- transaction semantics
- only want to look at order of reads and writes.
- equivalent to serial execution regardless of
- create dependency graph based on reads and writes required by each transaction
- if no cycles in graph, then the schedule of operations is equivalent to a serial schedule
Lecture 12 - Transaction Concurrency Control Cont’d
- Transaction
- a sequence of \(r_i(x)\) and \(w_i(x)\) actions
- Conflicting actions
- when \(i\) is different for read or write actions on the same piece of data.
- When two write operations at different points operate on the same data.
- Schedule
- represents chronological order in which actions are executed
- Serial Schedule
- no interleaving of actions or transactions.
- S1 and S2 are conflict equivalent schedules if S1 can be transformed into S2 by a series of swaps on non-conflicting actions.
- a schedule is conflict serializable if it is conflict equivalent to a serial schedule.
- A precedence graph \(P(S)\) where \(S\) is a schedule
- nodes are transactions in S
- edges: \(T_i\rightarrow T_j\) whenever
- \(p_i(A), q_j(A)\) are actions in S
- \(p_i(A) <_s q_j(A)\).
- at least one of \(p_i,q_i\) is a write.
Exercise: What is P(S) for $$S=w_3(A)w_2(C)r_1(A)w_1(B)r_1(C)w_2(A)r_4(A)w_4(D)
- edges:
- T3->T1
- T3->T4
- T1->T2
- T2->T4
- T1->T2
- conflict serializable if there is a cycle
- Lemma: S1,S2 conflict equivalent if P(S1) = P(S2)
- How to prove?
- assume they are not equivalent. List all edges. They are not equivalent if edges are different.
- if two graphs have equivalent precedence, doesn’t necessarily imply conflict equivalence
- if P(S1) is acyclic (no cycles) –> S1 is conflict serializable
- proof: Assume S1 is conflict serializable
- therefore, another schedules \(S_s\) is conflict equivalent to S1
- \(P(S_1) = P(S_s)\).
- \(P(S_1)\) is acyclic since \(P(S_s)\) is acyclic
- therefore, another schedules \(S_s\) is conflict equivalent to S1
- assume P(S1) is acyclic
- transform S1 as follows
- Take T1 to be transaction with no incident (incoming) arcs
- move all T1 actions to the front.
- repeat again discarding node T1
- transform S1 as follows
- proof: Assume S1 is conflict serializable
- how to enforce serializable schedules?
- option 1: run system, recording P(S). Check P(S) for cycles and declare if execution was good, or abort transactions as soon as they generate a cycle.
- option 2: prevent P(S) cycles from occurring via a scheduler that receives
all transactions.
- requires a locking protocol to prevent bad concurrent transactions
- \(l_i(A)\) - exclusive lock on A
- \(u_i(A)\) - unlock A
- scheduler reads lock table.
- may only operate on items which have locks
- still doesn’t fully solve the problem, because locks don’t prevent cycles
- 2-phase locking for transactions required.
- basic rule: once first unlock occurs, cannot unlock again.
- requires a locking protocol to prevent bad concurrent transactions
- Assume deadlocked transactions are rolled back
- have no effect
- do not appear in schedule
- beyond a 2PL protocol, it is about improving performance and allowing
concurrency -> other methods
- shared locks
- multiple granularity
- inserts, deletes, phantoms
- other types of concurrency control mechanisms
- shared locks – allowed on reads. multiple transactions can lock an item at the same time.
- transactions which read and write same object:
- option 1: request exclusive lock
- option 2: upgrade (need to read, but unsure about write)
- transactions which read and write same object:
Lecture 13 - Concurrency Control Cont’d
- Concurrency Control judged on few aspects
- how performant
- allow as many transactions as possible to occur in parallel
- Increment locks
- atomic increment action
- hardware ensures read and write executes atomically.
| Shared | Exclusive | Increment | |
| Shared | T | F | F |
| Exclusive | F | F | F |
| Increment | F | F | T |
- common table schema in practice:
CREATE TABLE T(attr SERIAL PRIMARY KEY,..);- prevents needing to lock the counter on attr.
- locking in practice
- don’t trust transactions to request/release locks
- hold all locks until transaction commits
- scheduler uses a lock table for which transactions for determining who needs or wants locks.
- lock table
- table of every possible object that can be locked
- null if unlocked, otherwise lock into for the object,
- locking work in most cases, but should we lock at large or fine
grain?
- large objects (e.g. relations)
- need new locks, low concurrency
- lock small objects (tuples, fields)
- more locks, more concurrency
- high overhead
- large objects (e.g. relations)
- table of every possible object that can be locked
- Share intentions about which locks to get, but don’t request them yet
- IS (Intend Shared)
- IX (Intend Exclusive)
- SIX (Shared Intend Exclusive)
| Parent Lock (table) | Child Locked In (tuple) |
|---|---|
| IS | IS, S |
| IX | IS, S, IX, X, SIX |
| S | [S, IS] not necessary |
| SIX | X, IX, [SIX] |
| X | None |
Rules:
- follow multiple granularity comp functions
- lock root of tree first, any mode
- node Q can be locked by a transaction in S or IS only if the parent is locked by IX or IS
- Node Q can be locked by a transaction in X, SIX, or IX only if the parent is locked by IX or SIX
- the transaction is a two phase locking process
- transaction can unlock node Q only if none of Q’s children are locked by the transaction
Handling Inserts and Deletes
- get exclusive lock on A before deleting
- At insertion of A on transaction, given exclusive lock to A on insertion
- Still have issue: Phantoms:
- can have serialized transactions without proper locks update same attr twice (e.g. unique instead)
- instead of locking on R, lock on an index of R
- generalize to tree-based concurrency control
- increase concurrency 0 don’t need to lock whole table
- generalized tree-based concurrency control
- all objects accessed through root
- follow pointers
- lock parent, then child, then grandchild, etc
- rules: tree protocol
- first lock by a transaction may be on any item
- after that, Q may be locked by any transaction only if the parent of Q was locked by the transaction
- items may be unlocked at any time
- after a transaction unlocks Q, it cannot relock Q.
Lecture 14 - More Concurrency Control and Transactions
- Transactions have 3 phases
- read
- all DB values read
- writes to temp storage
- no locking
- validate
- check is schedule so far is serializable
- write
- if validate ok, write to DB
- read
- key idea –> make sure validation is atomic
-
if T1, T2, T3, etc.. is validation order, then resulting scheduling will be conflict equivalent to S = (T1)(T2)(T3)
- to implement transaction validation - system has two sets
- FIN –> Transactions that have finished phase 3 (completed)
- VAL –> transactions that have successfully finished phase 2 (validation)
- validation rules for Tj
- when Tj starts phase 1:
- ignore(Tj) <– FIN
- at Tj validation:
- if check(Tj) then
- V <– \(V \cup T_j\)
- do write phase
- FIN <– FIN \(\cup T_j\)
- if check(Tj) then
- when Tj starts phase 1:
- implementation of
check(Tj)for Ti in VAL -IGNORE (Tj) DO IF ( WS(Ti) intersectes RS(Tj) != empty set OR Ti not in FIN ) THEN RETURN false RETURN true - This method is called “optimistic concurrency control”
- assumes that conflicts are rare
- system resources plentiful
- have real-time constraints
Concurrency Control and Recovery
- Two transactions, Ti and Tj write/read to same relation
- Tj writes first
- Ti reads after the write, and then commits.
- Tj then aborts at the end.
- without proper validation, would need a cascading rollback because Ti would have read data that technically wouldn’t have existed (the write from Tj)
- a schedule is recoverable is each transaction commits only after all transactions from which it read are committed
- A schedule avoids cascading rollback if each transaction may only read those values written by committed transactions -
Lecture 15 - Virtual and Materialized Views
Virtual view
CREATE VIEW V as
SELECT G, SUM(A) as S
FROM R
GROUP BY G
Materialized View
CREATE MATERIALIZED VIEW V as
SELECT G, SUM(A) as S
FROM R
GROUP BY G
| Virtual View | Materialized View | |
|---|---|---|
| When updating R | Database does nothing | Ideally, DB refreshes V to reflect changes of R |
| When querying V | optimize and run query that view represents | simply use the view as the base table |
- essentially, its up to the DB implementation to update a materialized view when its underlying tables are queried. This is called Incremental View Maintenance (IVM)
-
views only represent algebraic expressions and are simply re-evaluated upon every query. Kind of like an alias.
- At the end of a transaction which updates the relation R that a materialized view depends on, must be reflected in any materialized views which depend on the relation R.
- Two options
- delete and recompute view
- incrementally maintain view
- Two options
-
Capturing IVM as a computation of the changes of views
- neglect update commands
- think of update as a delete - insert
- Capture transaction as two delta tables \(\Delta R^+\) and \(\Delta R^-\)
- compute tuples to be deleted from view as \(\Delta V^-\) and \(\Delta V^+\)
-
delete \(\Delta V^-\) from V, and insert \(\Delta V^+\) into V
- IVM - Eager version
- problem: find efficient view updates after every table update
- IVM - deferred version
- allows choice of how long after transaction the DB updates a view
- IVM - self-maintaining
- works for some views
- typically, view change will require the delta of the R, the old view, and the new relation state.
- self-maintaining views don’t need the current state of the table to compute the new view.
- Basic IVM Algorithm
- Rule for \(V = R\bowtie S\)
- \[\Delta V^+ = ((\Delta R^+\bowtie S) \cup (R \bowtie \Delta S^+)) - (\Delta R^+ \bowtie \Delta S^+)\]
- \[\Delta V^- = (()) - ()\]
- Rule for \(V = \sigma_c R\)
- \[\Delta V^+ = \sigma_c \Delta R^+\]
- Compose the above rules to do IVM for more complex view queries
- \[\Delta V^- = \sigma_c \Delta R^-\]
- e.g. \(V = T \bowtie \sigma_{A > 5}W\)
- dumb way - compute two separate views by decomposing the views, then combine the views (inefficient)
- for above example
- \[\Delta V^+ = ((\Delta T^+ \bowtie \sigma_{A>5} W) \cup (T \bowtie \sigma_{A>5}\Delta W^+)) - (\Delta T^+ \bowtie \sigma_{A>5}\Delta W^+)\]
- Rule for \(V = R\bowtie S\)
- IVM with caching
- associate intermediate views (caches) with subexpressions
- bottom up: from updating caches to reaching the materialized view
- caches will typically need indices
- caches may or may not pay off as they incur a maintenance cost.
Lecture 15 - Query Processing …Again
- wong-yussefi algorithm (INGRES)
- optimize queries with lots of joins.
- smart exhaustive algorithm for plans
- textbook sec 16.6
- INGRES is a heuristic for plan enumeration
- not typically in use for modern databases
- exponential algorithm ok in practice as long as the exponent is low
- not typically in use for modern databases
- basic DP approach to enumerating plans
- for each sub expression \(op(e_1 e_2\dots e_n\)
- recursively compute the best plan and cost for each subexpression \(e_i\)
- for each physical operator \(op^p\) of each operator (\(op\))
- evaluate the cost of computing the operator abd bite best plan for each subexpression
- memo the best physical operator \(op^4\)
- for each sub expression \(op(e_1 e_2\dots e_n\)
Example
Given a query
SELECT *
FROM R, S, T, U
WHERE R.A = S.A AND R.B = S.B and T.C=U.C
Algorithm would
- give all plans
- eliminate all plans with a cartesian product and with only joins
- physical plans emerge from the above logical plans
- join types:
- Hash Join
- Merge join
- SSM
- S_M
- _SM
- each logical plan will have a number of physical plans because each
operator can have different physical implementations which run at
different speeds due to table layouts (partitions, indices, storage,
etc)
- number of plans grow large due to max implementations
- memoizing can reduce need to re-calculate costs.
- solving 3-way sub problems
- e.g. \(R\bowtie S \bowtie T\)
- split into single problems (e.g. parenthesis –> \((R\bowtie S) \bowtie T\) or \(R \bowtie (S\bowtie T)\))
- e.g. \(R\bowtie S \bowtie T\)
Local suboptimality of the basic approach, and the Selinger improvement
- basic dynamic programming may lead to globally suboptimal solutions
- solution good for one operation, but not for the whole query
- a suboptimal plan for \(e_1\) may lead to the optimal plan for an entire op
\(op(e_1 e_2\dots e_n)\)
- consider \(e_1 \bowtie e_2\)
- optimal computation of \(e_1\) produces an unsorted result
- optimal merge is a sort-merge join on A
- could have paid off to consider the suboptimal computation of \(e_1\) that produces sorted results on A
- Selinger improvement
- memo any plan that also produces an ordering of the results which may be of use to ancestor operators.